Unsere Welt verändert sich ständig, manchmal periodisch wie die Helligkeit oder die Temperatur im Laufe der Tage, manchmal (weitgehend) gleichmäßig wie der zurückgelegte Weg bei einem Jogger oder der Wasserstand in der Badewanne, wenn man den Wasserhahn aufgedreht hat. Pflanzen wachsen, Kinder wachsen, die Anzahl der Menschen auf der Erde wird immer größer, eine heiße Tasse Kaffee kühlt sich im Laufe der Zeit ab, eine brennende Kerze wird immer kleiner, …
Wenn die Veränderungen durch Zahlen messbar sind, kann man versuchen, dafür Funktionen zu finden. Periodische Veränderungen lassen sich mit Hilfe der trigonometrischen Funktionen beschreiben.
Um Funktionen 
für andere Wachstumsvorgänge zu entwickeln, sind ein paar Begriffe nützlich.
Den Funktionswert an der Stelle 
, also 
nennt man den Anfangswert oder Anfangsbestand des Wachstumsprozesses. Dieser hängt davon ab, zu welchem Zeitpunkt gesetzt wird.
Um die Veränderung zu beschreiben, die bei fortschreitender Zeit eintritt, untersuchen wir, wie sich die Funktion 
jeweils eine Zeiteinheit später entwickelt hat. Zur Beschreibung dieser Veränderung gibt es zwei Möglichkeiten:
- Der Summand
, um den die Funktion 
zunimmt, heißt Wachstumsrate (oder Änderungsrate). - Der Faktor
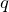, mit dem die Funktion zunimmt, wird Wachstumsfaktor genannt.
Zwei Wachstumsvorgänge treten besonders häufig auf:
Beim linearen Wachstum ist der Summand konstant. Die Funktion ist linear mit der Steigung .
Ein Beispiel:
Beim exponentiellen Wachstum ist der Faktor konstant. Im Beispiel ist der Anfangswert 
. Weil jedesmal mit 
multipliziert wird, ergeben sich die weiteren Funktionswerte 
, 
, 
, …
Das entspricht aber einer Exponentialfunktion mit 
.
Daneben gibt es noch andere Arten von Wachstumsvorgängen wie zum Beispiel beschränktes Wachstum, bei dem eine Größe nicht über eine bestimmte Schranke wachsen kann. Prozesse, bei denen eine Größe abnimmt wie etwa beim radioaktiven Zerfall, werden im erweiterten Sinn auch als Wachstumsfunktionen bezeichnet.