Dieser Beitrag ist Teil 2 von 7 in der Reihe 2.5 Exponentialfunktionen
- Wachstum
- Zinseszins
- Exponentialfunktion
- Die eulersche Zahl
- e-Funktionen
Exponentialfunktionen spielen eine große Rolle bei Wachstumsvorgängen in der Natur, Technik und Wirtschaft.
Die Funktionsgleichung einer Exponentialfunktion 
ist 
. Die Basis 
sollte positiv sein.
Aufgabe
- Verändere den Wert von 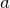und beobachte. Warum darf 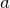nicht negativ sein?
- Die Funktionen zeigen unterschiedliches Monotonieverhalten (Steigen und Fallen). Wovon hängt das ab?
- Wie verändern sich die
-Werte, wenn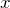 
um 
zunimmt? - Beschreibe die gemeinsamen Eigenschaften aller Exponentialfunktionen.
- Gib die Definitions- und Wertemenge der Exponentialfunktionen an.
- Wie verhalten sich die Graphen für
und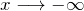 
Dr. Marie-Luise Herrmann, erstellt mit GeoGebra