Modellieren von Wachstum

Dieser Beitrag ist Teil 7 von 7 in der Reihe 2.5 Exponentialfunktionen

2.5 Exponentialfunktionen

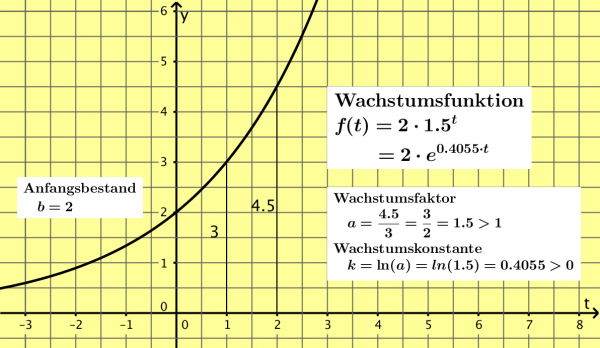
Exponentielles Wachstum lässt sich beschreiben durch eine Exponentialfunktion der Form $f(t)=b\cdot a^t$ ;

dabei ist $a$ der Wachstumsfaktor und $b$ der Anfangsbestand (siehe auch den Beitrag Wachstum). Anstelle der Variablen $x$ wird meistens $t$ (für die Zeit) verwendet.

Wenn $a>1$ ist, liegt exponentielles Wachsen vor. Ist dagegen $a<1$ , handelt es sich um exponentielles Fallen oder exponentielle Abnahme.

Wegen $a=e^{\ln(a)}$ kannst du den Wachstumsprozess auch durch eine e-Funktion beschreiben. Mit $k=\ln(a)$ erhältst du dann $f(t)=b\cdot e^{k\cdot t}$ .

Wenn $k>O$ ist, heißt $k$ Wachstumskonstante und $f$ Wachstumsfunktion.

Wenn $k<O$ ist, heißt $k$ Zerfallskonstante und $f$ Zerfallsfunktion.

Aufstellen von Wachstums- und Zerfallsfunktionen

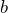$b$ ist der Anfangsbestand zum Beginn der Beobachtung $b=f(0)$ .
Der Wachstumsfaktor (oder Zerfallsfaktor) ergibt sich als Quotient zweier aufeinanderfolgender Bestände: $a=\frac{f(t+1)}{f(t)}$
Damit erhältst du die Wachstumsfunktion (oder Zerfallsfunktion) $f(t)=b\cdot a^t$ .
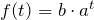Mit 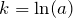$k=\ln(a)$ erhältst du die Wachstums- oder Zerfallsfunktion als $e$ -Funktion: $f(t)=b\cdot e^{k\cdot t}$ .

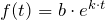Beschränktes Wachsen und Fallen

Es gibt in der Natur häufig Wachstumsprozesse, die nur am Anfang exponentiell verlaufen. Werden zum Beispiel in einem See Fische ausgesetzt, so können diese sich zunächst stark vermehren, irgendwann aber werden die Nahrungsmittel für eine immer größer werdende Population nicht mehr ausreichen.

Solche Wachstumsprozesse nennt man beschränktes Wachstum. Dabei gibt es eine obere Schranke $S$ , die nicht überschritten werden kann (in dem Beispiel mit den Fischen wäre es die maximale Anzahl an Fischen, die der See ernähren kann). Beschränktes Wachstum kann durch eine Funktion $f$ mit $f(t)=S-b\cdot a^t$ mit $0<a<1$ beschrieben werden. Wegen $a=e^{\ln(a)}$ kann die Funktion auch mit der Basis $e$ geschrieben werden.

Ein beschränkter Zerfall liegt zum Beispiel dann vor, wenn eine heiße Tasse Kaffee abkühlt. Die Zerfallsfunktion wäre dann eine Funktion $f$ mit $f(t)=S+b\cdot a^t$ mit $0<a<1$ , die man auch wieder mit der Basis $e$ angeben kann.

Reihen Navigation<< Der Logarithmus

Aufstellen von Wachstums- und Zerfallsfunktionen

Beschränktes Wachsen und Fallen

Schreibe einen Kommentar Antworten abbrechen