- Das Programm GeoGebra
- GeoGebra-Arbeitsblatt
- Lineare Gleichungssysteme
- Anfang mit GeoGebra
- Geometrie und Werkzeuge
LGS mit zwei Unbekannten
Eine lineare Gleichung mit zwei Variablen kann auf die Form 
gebracht werden (dabei dürfen nicht beide Variablen a und b den Wert 0 haben). Eine solche Gleichung entspricht grafisch einer Geraden; jeder Punkt dieser Geraden bildet ein Lösungspaar (x, y) der Gleichung. Es gibt also unendlich viele Lösungen.
Kommt jetzt eine zweite Gleichung hinzu, erhalten wir ein lineares Gleichungssystem (kurz LGS). Ein Zahlenpaar (x, y) heißt Lösung des LGS, wenn das Paar jede Gleichung des Systems erfüllt.
In dem GeoGebra-Applet ist zunächst eine Gleichung mit zwei Unbekannten als Gerade dargestellt. Klicke auf den Punkt in der zweiten Zeile und du erhältst die Gerade für die zweite Gleichung. Die Lösung dieses LGS wird durch den Schnittpunkt der beiden Geraden dargestellt. Du kannst ihn auch mit dem CAS-Befehl Löse erhalten.
Dr. Marie-Luise Herrmann, erstellt mit GeoGebra
LGS mit mehr Unbekannten
Es gibt auch lineare Gleichungssysteme mit mehr Unbekannten. Ein Beispiel:
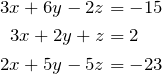
Beim Gauß-Verfahren (auf dieser Seite findest du einen kleinen Überblick) lässt sich das LGS mithilfe von elementaren Zeilenumformungen überführen in die Stufenform, die sehr viel leichter zu lösen ist:
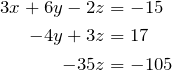
Zur Lösung des LGS kannst du dann in der letzten Zeile beginnen und dich dann nach oben „durchkämpfen“. Im nächsten Abschnitt erfährst du, wie GeoGebra LGS Gleichungen löst.