LGS lösen mit einer Matrix

Dieser Beitrag ist Teil 16 von 18 in der Reihe GeoGebra-Kurs

GeoGebra-Kurs

Auf der Seite Lineare Gleichungssysteme haben wir als Beispiel das LGS

$\begin{align*}3x+6y-2z&=-15\\3x+2y+z&=2\\2x+5y-5z&=-23\end{align*}$

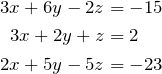
kennengelernt. Diesem LGS entspricht die erweiterte Koeffizientenmatrix:

$\begin{pmatrix}3&6&-2&-15\\3&2&1&2\\2&5&-5&-23\end{pmatrix}$

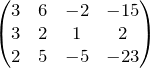
Bei einer Koeffizienzenmatrix lassen sich die gleichen Zeilenumformungen durchführen wie bei einem normalen LGS. So könnte man dann die Matrix

$\begin{pmatrix}3&6&-2&-15\\0&-4&3&17\\0&0&-35&-105\end{pmatrix}$

erhalten, die der Stufenform entspricht. Wenn man noch weitere Zeilenumformungen vornimmt, kann man zu der Form

$\begin{pmatrix}1&0&0&1\\0&1&0&-2\\0&0&1&3\end{pmatrix}$

gelangen. Diese Form heißt auch die reduzierte Stufenform oder Treppennormalform. GeoGebra kennt diese auch:

Aus der Treppennormalform lassen sich die Lösungen unmittelbar ablesen: x = 1, y = -2 und z = 3. Genial einfach!